Cosmology

Fate of the Universe

Chapter index in this window — — Chapter index in separate window

This material (including images) is copyrighted!. See my copyright notice for fair use practices.

Now that you have explored the beginnings of the universe and have an answer to the question ``where did we come from?'', let's address the other question, ``where are we going?'' This final section will cover the fate of the universe. We observe that the universe is expanding and that gravity is slowing it down. Which of them will win?

Depends on Mass (Curvature of Space)

The more mass there is, the more gravity there is to slow down the expansion. Is there enough gravity to halt the expansion and recollapse the universe or not? If there is enough matter (gravity) to recollapse the universe, the universe is ``closed''. In the examples of curved space above, a closed universe would be shaped like a four-dimensional sphere (finite, but unbounded). Space curves back on itself and time has a beginning and an end. If there is not enough matter, the universe will keep expanding forever. Such a universe is ``open''. In the examples of curved space, an open universe would be shaped like a four-dimensional saddle (infinite and unbounded). Space curves away from itself and time has no end.

curvature and possible fates of the universe

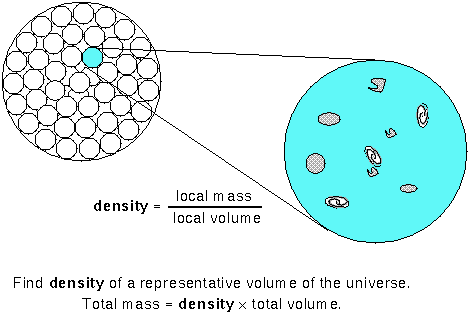
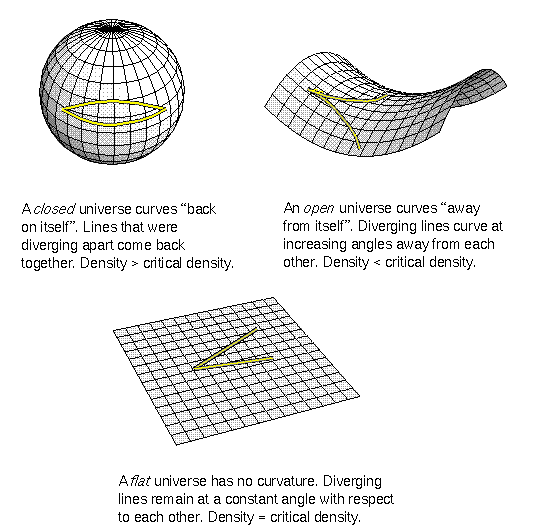
Instead of trying to add up all of the mass in the universe, a more reasonable thing to do is to find the density of a representative region of the universe. The density = (mass in the region)/(volume of the region). If the region is truly representative, then the total mass of the universe = the density × the total volume of the universe. If the density is great enough, then the universe is closed. If the density is low enough, then the universe is open. In the popular astronomy magazines, you will probably see the mass density of the universe specified by the symbol ``''. It is the ratio of the current density to the ``critical density'' described in the next paragraph. If < 1, the universe is open; if > 1, the universe is closed.

measuring the density of our neighborhood to determine the fate of the universe

Critical Density

The boundary density between the case where the universe has enough mass/volume to close universe and too little mass/volume to stop the expansion is called the critical density. The critical density = 3H²/(8

G), where H is the Hubble constant for a given cosmological time. Notice that the Hubble constant has appeared again! It measures the expansion rate, so it should be in the critical density relation. The current critical density is approximately 1.06 × 10^-29 g/cm³. This amounts to six hydrogen atoms per cubic meter on average overall.

A critical density universe has ``flat'' curvature. The density parameter equals exactly 1 in a flat universe. The Hubble ``constant'' is not really a constant—it is different at different cosmological times. The greater the value of the Hubble constant at a given cosmological time, the faster the universe is expanding at that time. Gravity slows the expansion of the universe, so the early universe was expanding faster than it is now. That means that the critical density was greater at earlier times. It changes by the same factor that the actual density of the universe changes throughout the expansion. So if the universe starts out with a density greater than the critical density, then its density will always be greater than critical density. If the universe starts out with a density less than the critical density, then its density will always be less than the critical density.

Go back to previous section -- Go to next section

Go to Astronomy Notes home

last updated: June 28, 2022

Is this page a copy of Strobel's Astronomy Notes?

Author of original content: Nick Strobel