Video lecture for this chapter
The ability of a telescope to enlarge images is the best-known feature of a telescope. Though it is so well-known, the magnifying power is the least important power of a telescope because it enlarges any distortions due to the telescope and atmosphere. A small, fuzzy faint blob becomes only a big, fuzzy blob. Also, the light becomes more spread out under higher magnification so the image appears fainter! The magnifying power = (focal length of objective) / (focal length of eyepiece); both focal lengths must be in the same length units. A rough rule for the maximum magnification to use on your telescope is 20 × D to 24 × D, where the objective diameter D is measured in centimeters. So an observer with a 15-centimeter telescope should not use magnification higher than about 24 × 15 = 360-power.
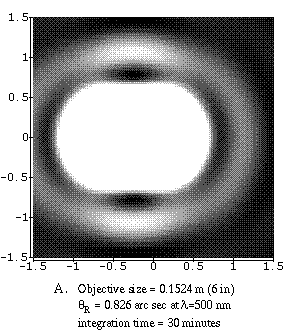
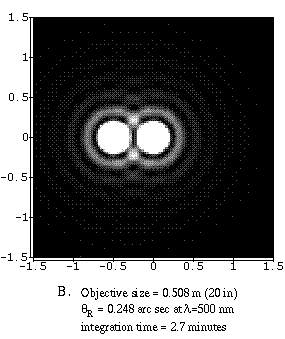
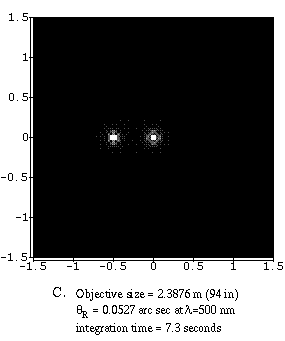
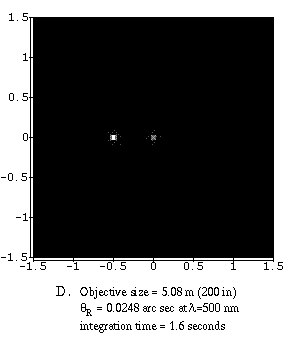
The set of four figures below shows the effect of a larger objective
size. They have the same magnification. These are
ideal images of two stars separated by 0.5
arc seconds which would be the angular separation for stars at the Sun and
Jupiter's positions if the system was 33 light years from us. The frames
are 1.5 arc seconds square and are at the observation wavelength of
500 nanometers. The resolving power is given by
and they all have the same
brightness---the light in the bottom images from the large telescopes is just
much more concentrated than for the small telescopes. The image from the 0.1524-meter
telescope (image A) would take 30
minutes to make, but the image from the 5.08-meter telescope (image D) would
take only 1.6 seconds! The exposure times for the other telescopes are given.
The pictures clearly show the increase in sharpness as the objective size is increased. The size of each of the blobs is the size of the smallest detail that can be seen with that telescope under ideal conditions. Atmospheric distortion effects (smearing of the binary star images to a blob the size of the entire frame) and obscuration and diffraction by the secondary and its supports are NOT shown here.
Go back to previous section --
Go to next section
last updated: January 19, 2022