This material (including images) is copyrighted!. See my copyright notice for fair use practices.
At first you might think that in order to understand the structure of something as large as the universe, which by definition contains everything there is, you would need some very powerful telescope to see to the farthest reaches of space and a complex theoretical model. Actually, there are some powerful conclusions you can draw from observations with the naked eye. You will explore that first and then move on to conclusions you can draw from extending your eyesight. You will explore the basic questions that human beings have been asking themselves ever since we have walked the Earth: where did we come from and where are we going?
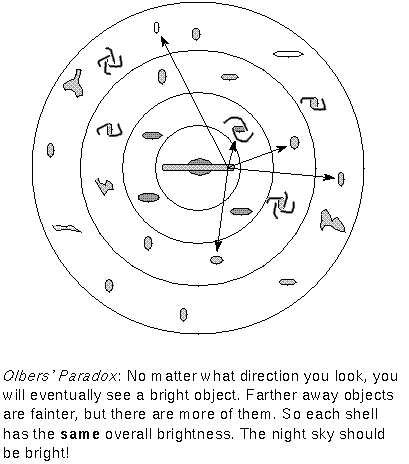
If the universe is uniformly filled with stars, then no matter which direction you look, your line of sight will eventually intersect a star (or other bright thing). Now it is known that stars are grouped into galaxies, but the paradox remains: your line of sight will eventually intersect a galaxy.

The brightnesses of stars does decrease with greater distance (remember the inverse square law) BUT there are more stars further out. The number of stars within a spherical shell around us will increase by the same amount as their brightness decreases. Therefore, each shell of stars will have the same overall luminosity and because there are a lot of ever bigger shells in an infinite universe, there is going to be a lot of light!
Any intervening material absorbing the starlight would eventually heat up and radiate as much energy as it absorbed, so the problem remains even if you try these "shields". Of course, stars are not points. They do have a definite size, so they can block light from other stars. The total brightness of the universe will not be infinite, but only as bright as the surface of a star (!). You can substitute "galaxy" for "star" in the preceding paragraphs if you want to update Olbers' Paradox for modern times. The way to resolve a paradox like this is to look at the assumptions that are used (the "if" statements) and determine whether or not they are valid.
Georges Lemaître and Albert Einstein
In 1915 Albert Einstein published his Theory of General Relativity that described gravity as a curvature of spacetime (see the Relativity chapter). In 1917 Einstein applied General Relativity to the universe as a whole and showed that the universe must either expand or contract. Since there was no evidence of such large-scale motion, he added a term to the equations called the "cosmological constant" to keep the universe static. Alexander Friedman (lived 1888 - 1925) in 1922 and then the Belgian priest/astrophysicist Georges Lemaître (lived 1894 - 1966) in 1927 (independent of Friedman) used General Relativity to show that the universe must be expanding. In his 1927 paper Lemaître suggested a relation between the galaxy speeds and distances like what Edwin Hubble would later observe. Einstein disagreed with Lemaître but Lemaître persevered. Einstein would later come to agree with Lemaître on the expansion of the universe arising from General Relativity after Edwin Hubble announced his observations in 1929 that the universe is not static---it is expanding. In later papers and conferences Lemaître argued for a beginning to the universe that would later become the Big Bang Theory described more fully later in this chapter. In 1933 Einstein agreed that Lemaître was correct. [There is now evidence that Lemaître actually derived a value for the Hubble constant using some early distance measurements of Hubble and Slipher's redshifts in his 1927 paper but his work is less well-known than Hubble's because the paper was published in an obscure journal (Annales de la Societe scientifique de Bruxelles) written in French while Hubble's paper (with Milton Humason) in 1931 with better distance data laying out the case for the galaxy motions first announced in 1929 appeared in the more widely-read Astrophysical Journal and the English translation of Lemaître's paper in a 1931 issue of Monthly Notices of the Royal Academy of Sciences did not have that derivation of the Hubble constant. It was probably the more convincing observational evidence laid out in the Hubble & Humason paper that led Einstein to admit that Lemaître was correct all along.]
The expansion is enough to resolve the paradox. As the universe expands, the light waves are stretched out and the energy is reduced. Also, the time to receive the light is also lengthened over the time it took to emit the photon. Because the luminosity = the energy/time, the apparent brightness will be reduced enough by the expansion to make the sky dark.
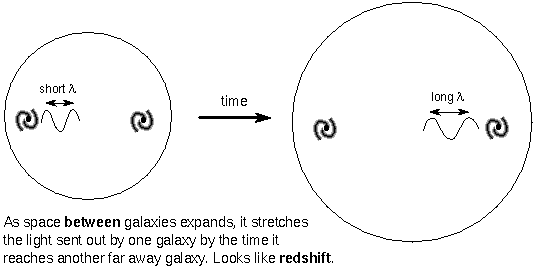
The stretching of the light waves makes the light from galaxies appear redshifted, mimicking a redshift from the doppler effect as if the galaxies were moving through space away from us. However, the galaxies are simply being carried along with the expansion of the space between them---the whole coordinate system is expanding. The expansion of the universe means that galaxies were much closer together long ago. This implies that there is a finite age to the universe, it is not eternal. Even if the universe is infinite, the light from places very far away will not have had enough time to reach us. This will make the sky dark.
The Hubble-Lemaître law, speed = Ho × distance, says the expansion is uniform. The Hubble constant, Ho, is the slope of the line relating the speed of the galaxies away from each other and their distance apart from each other. It indicates the rate of the expansion. If the slope is steep (large Ho), then the expansion rate is large and the galaxies did not need much time to get to where they are now. If the slope is shallow (small Ho), then the galaxies need a lot of time to get to where they are now.
The age of the universe can be easily estimated from the simple relation of time = distance/speed. The Hubble-Lemaître Law can be rewritten 1/Ho = distance/speed. Notice that the expansion time interval = 1/Ho. The Hubble constant tells you the age of the universe, i.e., how long the galaxies have been expanding away from each other: Age = 1/Ho. This value for the age is an upper limit since the expansion has been slowing down due to gravity. That means that the Hubble "constant" actually was larger in the past. Taking the expansion slowdown into account, you get an age closer to 2/(3 Ho). Still, the age looks like a number × (1/Ho), so if the Hubble constant is large, the derived age of the universe will be small.
![]() Go back to previous section --
Go back to previous section --
![]() Go to next section
Go to next section
last updated: June 28, 2022