 |
 |
There are several ways to figure out relative ages, that is, if one thing is older than another. For example, looking at a series of layers in the side of a cliff, the younger layers will be on top of the older layers. Or you can tell that certain parts of the Moon's surface are older than other parts by counting the number of craters per unit area. The old surface will have many craters per area because it has been exposed to space for a long time. But how old is ``old''? If you assume that the impact rate has been constant for the past several billion years, then the number of craters will be proportional to how long the surface is exposed. However, the crater number relation must be calibrated against something with a known age.
To measure the passage of long periods of time, scientists take advantage of a regularity in certain unstable atoms. In radioactive atoms the nucleus will spontaneously change into another type of nucleus. When looking at a large number of atoms, you see that a certain fraction of them will change or decay in a certain amount of time that depends on the type of atom---more specifically, the type of nucleus. Radioactive dating is an absolute dating system because you can determine accurate ages from the number of remaining radioactive atoms in a rock sample. Most of the radioactive isotopes used for radioactive dating of rock samples have too many neutrons in the nucleus to be stable.
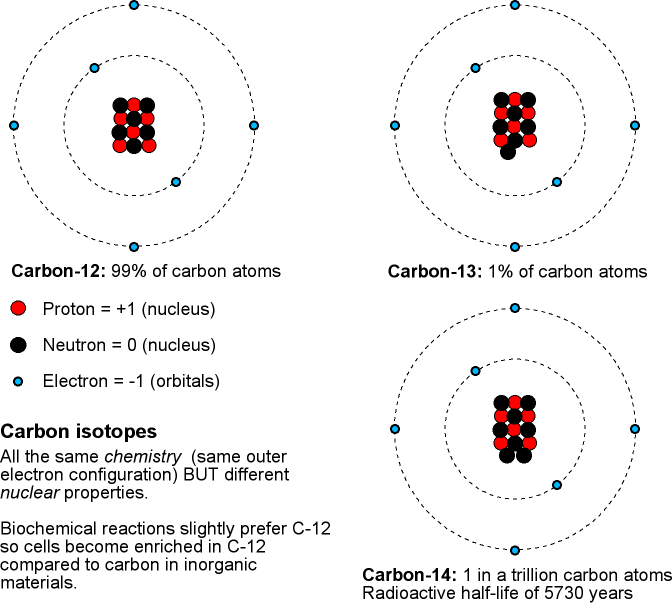
Recall that an isotope is a particular form of an element. All atoms of an element have the same number of protons in their nucleus and behave the same way in chemical reactions. The atoms of an isotope of a given element have same number of protons AND neutrons in their nucleus. Different isotopes of a given element will have the same chemistry but behave differently in nuclear reactions. In a radioactive decay, the original radioactive isotope is called a parent isotope and the resulting isotope after the decay is called a daughter isotope. For example, Uranium-238 is the parent isotope that breaks apart to form the daughter isotope Lead-204.
 |
 |
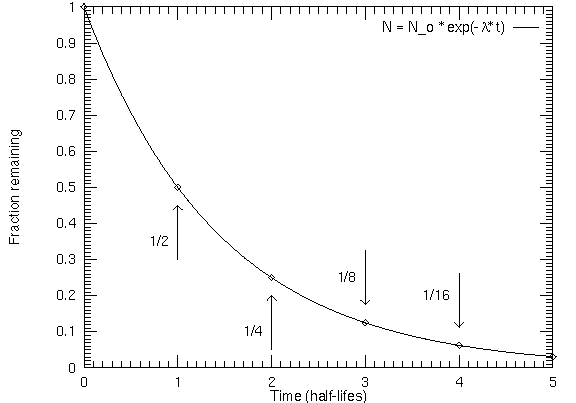
Radioactive isotopes will decay in a regular exponential way such that one-half of a given amount of parent material will decay to form daughter material in a time period called a half-life. A half-life is NOT one-half the age of the rock! When the material is liquid or gaseous, the parent and daughter isotopes can escape, but when the material solidifies, they cannot so the ratio of parent to daughter isotopes is frozen in. The parent isotope can only decay, increasing the amount of daughter isotopes. Radioactive dating gives the solidification age. When the rock melts, the radioactive dating "clock" gets reset.
There are two simple steps for radioactive dating:
How do you do that?If 1/8 of the original amount of parent isotope is left in a radioactive sample, how old is the sample? Answer: After 1 half-life, there is 1/2 of the original amount of the parent left. After another half-life, there is 1/2 of that 1/2 left = 1/2 × 1/2 = 1/4 of original amount of the parent left. After yet another half-life, there is 1/2 of that 1/4 left = 1/2 × 1/2 × 1/2 = 1/8 of the original amount of the parent left (which is the fraction asked for). So the rock is 1 half-life + 1 half-life + 1 half-life = 3 half-lives old (to get the age in years, simply multiply 3 by the half-life in years). |
If you have a fraction that is not a multiple of 1/2, then it is more complicated. The age = [ln(original amount of parent material / current amount of parent material) / ln(2)] × (half-life in years), where ln() is the ``natural logarithm'' (it is the ``ln'' key on a scientific calculator).
One common sense rule to remember is that the number of parent isotope atoms + the number of daughter isotope atoms = an unchanging number throughout time. The number of parent isotopes decreases while the number of daughter isotopes increases but the total of the two added together is a constant. You need to find how much of the daughter isotopes in the rock (call that isotope ``A'' for below) are not the result of a radioactive decay of parent atoms. You then subtract this amount from the total amount of daughter atoms in the rock to get the number of decays that have occurred since the rock solidified. Here are the steps:
The oldest meteorites have ages clustering around 4.55 to 4.57 billion years with uncertainties in the age measurements of less than 100 million years. The narrow range of ages is taken to be how long it took the parent bodies of the meteorites to form.
The discussion above is for the case of determining when a rock solidified (and it is usually very old rocks!). To determine the ages of old, once-living material such as plants, then something like carbon-14 will be used. Most carbon atoms are carbon-12 (99%) or carbon-13 (1%). A very small fraction (about 1 part in 1012 ) are the radioactive carbon-14 isotope that will decay to form nitrogen-14 with a half-life of 5,730 years. Carbon-14 is being produced continuously in our atmosphere when cosmic rays (extremely high-energy particles from space, mostly protons) collide with air molecules. When plants absorb carbon-dioxide in the photosynthesis process, some of the carbon dioxide has the carbon-14 atom in the molecule. Assuming that our atmosphere's composition and the cosmic ray flux has not changed significantly in the last few thousand years, you can find the age of the once-living organic material by comparing its carbon-14/carbon-12 ratios to those of now-living plants. Carbon-14 dating works well for samples less than about 50,000 to 60,000 years old and for things that were getting their carbon from the air.
The American Astronomical Society and the Astronomical Society of the Pacific published a beautifully-illustrated guide for teachers, students, and the public called An Ancient Universe: How Astronomers Know the Vast Scale of Cosmic Time. (PDF document: 800 kb in size!) This guide for Teachers, Students and the Public was written by a subcommittee of the American Astronomical Society's Astronomy Education Board. This is a local copy from the AAS Education Board.
![]() Go back to previous section --
Go back to previous section --
![]() Go to next section
Go to next section
last updated: June 8, 2022