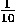= 1 × 10-1,
×
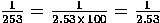10-2 or about 0.395 × 10-2 = 3.95 × 10-3.
For numbers larger than 10, the power of 10 is a positive value and negative for numbers less than 1. For numbers between 0 and 10, the power is a positive fraction. In the examples that follow, notice what happens to the decimal point:
| 100 = 1. | = | 1. with the decimal point moved 0 places |
| 101 = 10. | = | 1. with the decimal point moved 1 place to the right |
| 102 = 100. | = | 1. with the decimal point moved 2 places to the right |
| 106 = 1000000. | = | 1. with the decimal point moved 6 places to the right |
| and | | |
| 10-1 = 0.1 | = | 1. with the decimal point moved 1 place to the left |
| 10-2 = 0.01 | = | 1. with the decimal point moved 2 places to the left |
| 10-6 = 0.000001 | = | 1. with the decimal point moved 6 places to the left. |
The exponent of 10 tells you how many places to move the decimal point to the right for positive exponents or left for negative exponents. These rules come in especially handy for writing very large or very small numbers.
Since you will be working with very large and very small numbers, use scientific notation to cut down on all of the zeroes you need to write. Proper scientific notation specifies a value as a number between 1 and 10 (called the mantissa below) multiplied by some power of ten, as in
10 = 1 × 101, 253 = 2.53 × 100 = 2.53 × 102 and
15,000,000,000 = 1.5 × 1010
which you will sometimes see written as
15 × 109 even though
this is not proper scientific notation. For small numbers we have:
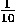= 1 × 10-1,
×
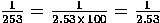10-2 or about 0.395 × 10-2 = 3.95 × 10-3.
When you divide two values given in scientific notation, divide the mantissa
numbers and subtract the exponents in the power of ten. Then adjust the
mantissa and exponent so that the mantissa is between 1 and 10 with the appropriate
exponent in the power of ten. For example:
×
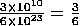1010-23 = 0.5 × 10-13 = 5 × 10-14.
Notice what happened to the decimal point and exponent in the examples. You subtract one from the exponent for every space you move the decimal to the right. You add one to the exponent for every space you move the decimal to the left.
Most scientific calculators work with scientific notation. Your calculator will
have either an ``EE'' key or an ``EXP'' key. That is for entering
scientific notation. To enter 253 (2.53 × 102),
you would punch 2 
.
5
3
EE or EXP
2. To enter
3.95 × 10-3,
you would punch
3 .
9
5
EE or EXP
3
[
key]. Note that
if the calculator displays ``3.53 -14'' (a space between the 3.53 and -14),
it means
3.53 × 10-14
NOT
3.53-14! The value of 3.53-14 = 0.00000002144 =
2.144×10-8 which is vastly different than the number
3.53×10-14. Also if
you have the number 4 × 103
and you enter 4
× 1
0
EE or EXP
3, the calculator
will interpret that as 4 × 10 × 103 = 4 × 104
or ten times greater than the number you really want!
One other word of warning: the EE or EXP key is used only for scientific notation
and NOT for raising some number to a power. To raise a number to some exponent
use the ``yx'' or ``xy'' key depending on the calculator. For example, to raise 3 to
the 4th power as in 34 enter
3 yx or
xy 4. If you instead
entered it using the EE or EXP key as in
3 EE or EXP
4, the calculator
would interpret that as 3×104 which is much different than 34 = 81.
Go back to previous section --
Go to next section
last updated: 27 May 2001