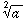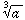Your web browser needs to be able to format superscripts for the
following sections! If the number ``106'' looks like ``106'', then
your web browser cannot format superscripts and the following will be a bit
confusing for that reason.
A shorthand way to express a quantity multiplied by itself one or more time
is to use a superscript number called an exponent. So
| a | = | a1 |
| a × a | = | a2 (not 2 × a!) |
| a× a × a | = | a3 (not 3 × a!) |
| a× a× a× a | = | a4 |
| a× a× a× a× a | = | a5 |
The quantity ``a squared'' means a2, ``a cubed'' means a3, and more
generally, ``a to the nth power'' is an.
Some special rules apply when you divide or multiply numbers raised to some
power. When you have an multiplied by am,
the result is a raised to a power that is the sum of the exponents:
an × am = an+m
When you have an divided by am, the result
is a raised to a power that
is the difference of the exponents---the exponent on the bottom is subtracted
from the exponent on the top:
(an) / (am) = an-m (not
am-n!)
When you have an raised to a power m, you multiply the
exponents:
(an)m = an × m = anm (not an+m!)
Negative exponents are used for reciprocals:
1 / a = a-1, 1 / (a2) =
a-2,
1 / (a3) = a-3, 1 / (a4)
= a-4, etc.
Scientific calculators have a ``yx'' key or a
``xy'' that takes care of
raising numbers to some exponent. Some fancy calculators have a ``^'' key
that does the same thing. Some calculators have ``x2'' and ``x3'' keys
to take care of those frequent squaring or cubing of numbers.
Check your calculator's manual or your instructor. The Basic Skills Computer
Lab has some excellent software that can improve your skills with exponents.
Try it out!
The square root of a quantity is a number that when multiplied by itself,
the product is the original quantity:
Sqrt[a] × Sqrt[a] = a.
Some examples: Sqrt[1] = 1 because 1 × 1 = 1; Sqrt[4] = 2 because
2 × 2 = 4; Sqrt[38.44] = 6.2 because 6.2 × 6.2 = 38.44;
Sqrt[25A2] = 5A because 5A × 5A = 25A2.
A square root of a number
less than 1, gives a number larger than the number itself:
Sqrt[0.01] = 0.1 because 0.1 × 0.1 = 0.01 and Sqrt[.36] = 0.6
because 0.6 × 0.6 = 0.36.
The cube root of a quantity is a number that when multiplied by itself
two times, the product is the original quantity:
Cube-Root[a] × Cube-Root[a] ×
Cube-Root[a] = a.
Scientific calculators have ``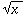 '' and
sometimes
``
'' and
sometimes
``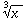 ''
keys to take care of the common square roots or cube roots. An expression
''
keys to take care of the common square roots or cube roots. An expression
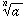 means the nth root of a.
How can you use your calculator
for something like that? You use the fact that the nth root of a is
a raised to a fractional exponent of 1/n. So we have:
means the nth root of a.
How can you use your calculator
for something like that? You use the fact that the nth root of a is
a raised to a fractional exponent of 1/n. So we have:
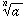 |
= | a1/n |
Sqrt[a] = 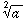 |
= | a1/2 |
Cube-root[a] = 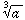 |
= | a1/3 |
When you raise some nth root to some power m, you simply multiply
the exponents as you did above for (an)m:
(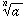 )m =
(a1/n)m
= a1/n × m = am/n.
So (a6)1/2 = a6× (1/2) =
a3 and (a1/2)6 =
a(1/2)× 6
= a3. But if you have a1/n multiplied
by am,
you add the exponents
since you are not raising a1/n to some power m:
a1/2 × a6 = a(1/2) + 6 =
a6 & 1/2 = a13/2.
)m =
(a1/n)m
= a1/n × m = am/n.
So (a6)1/2 = a6× (1/2) =
a3 and (a1/2)6 =
a(1/2)× 6
= a3. But if you have a1/n multiplied
by am,
you add the exponents
since you are not raising a1/n to some power m:
a1/2 × a6 = a(1/2) + 6 =
a6 & 1/2 = a13/2.
 Go back to previous section --
Go back to previous section --
 Go to next section
Go to next section
last updated: 27 May 2001
Is this page a copy of Strobel's
Astronomy Notes?
Author of original content:
Nick Strobel
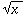 '' and
sometimes
``
'' and
sometimes
``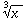 ''
keys to take care of the common square roots or cube roots. An expression
''
keys to take care of the common square roots or cube roots. An expression
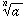 means the nth root of a.
How can you use your calculator
for something like that? You use the fact that the nth root of a is
a raised to a fractional exponent of 1/n. So we have:
means the nth root of a.
How can you use your calculator
for something like that? You use the fact that the nth root of a is
a raised to a fractional exponent of 1/n. So we have: