Inverse Square Law

Chapter index in this window —   — Chapter index in separate window

Video lecture for this chapter

This material (including images) is copyrighted!. See my copyright notice for fair use practices.

Newton's law of gravity describes a force that decreases with the SQUARE of the distance. For every factor of 2 the distance increases, the gravitational attraction decreases by a factor of 2 × 2 = 4; for every factor of 3 increase in distance, the gravity decreases by a factor of 3 × 3 = 9 (not by 3 + 3 = 6!); for every factor of 4 increase in distance, the gravity decreases by a factor of 4 × 4 = 16 (not by 4 + 4 = 8!), etc. See the mathematics review appendix for a review of ``factor'' and ``times''. Some more examples are given in the table below. Notice how quickly an inverse square law gets very small.

A comparison of inverse and inverse square relations
distance inverse inverse square
1 1/1 = 1 1/12 = 1
2 1/2 = 0.5 1/22 = 1/4 = 0.25
3 1/3 = 0.33 1/32 = 1/9 = 0.11
4 1/4 = 0.25 1/42 = 1/16 = 0.0625
7 1/7 = 0.14 1/72 = 1/49 = 0.02
10 1/10 = 0.1 1/102 = 1/100 = 0.01
100 1/100 = 0.01 1/1002 = 1/10,000 = 0.0001

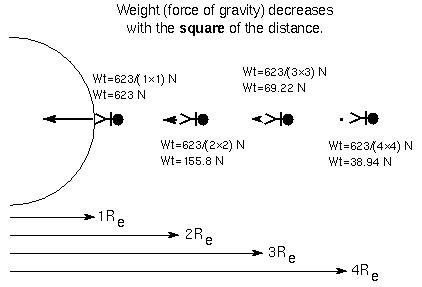
Example: Joe Average has a mass of 63.5 kilograms, so he weighs 623 newtons (=140 pounds) on the Earth's surface. If he moves up 1 Earth radius (= 6378 kilometers) above the surface, he will be two times farther away from the Earth's center (remember that distances are measured from center-to-center!), so his weight will be four times less, or 623/4 newtons = 155.8 newtons (= 140/4 pounds); NOT two times less, or 623/2 newtons = 311.5 newtons. If he moves up another Earth radius above the surface, he will be three times farther away than he was at the start, so his weight will drop by a factor of nine times, NOT 3 times. His weight will be 623/9 newtons = 69.22 newtons (= 140/9 pounds); NOT 623/3 newtons = 207.7 newtons. His mass will still be 63.5 kilograms. Figure below illustrates this.

Let us generalize this for any situation where the masses do not change: the force of gravity at distance A = (the force of gravity at distance B) × (distance B / distance A)2. Notice which distance is in the top of the fraction! To use this relation, have the gravity at distance A represent the unknown gravity force you are trying to find and the gravity at distance B represent the reference gravity force felt at the reference distance B.

inverse square law

How do you do that?

Let's find where the weight values in the inverse square law figure come from.
For Mr. Average's case the reference weight is his weight on the surface of the Earth = 623 N. His weight at 6378 kilometers above the surface is gravity at A = 623 × [6378/(2 × 6378)]2 = 623 × 1/22 = 623 × 1/4 = 155.8 N.
When he is at two Earth radii above the surface, the gravity at A = 623 × [6378/(3 × 6378)]2 = 623 × 1/32 = 623 × 1/9 = 69.22 N.

Formulae

Inverse Square Law: Gravity at A = gravity at B × (distance B / distance A)2.

Review Questions

  1. Why is gravity called an ``inverse square law''?
  2. What is the difference between a simple inverse relation and an inverse square relation?
  3. If the Earth was 3 A.U. from the Sun (instead of 1 A.U.), would the gravity force between the Earth and the Sun be less or more than it is now? By how many times?
  4. If Mercury was 0.2 A.U. from the Sun (instead of 0.4 A.U.), would the gravity force between Mercury and the Sun be less or more than it is now? By how many times?

previousGo back to previous section -- next Go to next section

Go to Astronomy Notes home

last updated: 11 May 2001

Is this page a copy of Strobel's Astronomy Notes?
Author of original content: Nick Strobel