This material (including images) is copyrighted!. See my copyright notice for fair use practices.
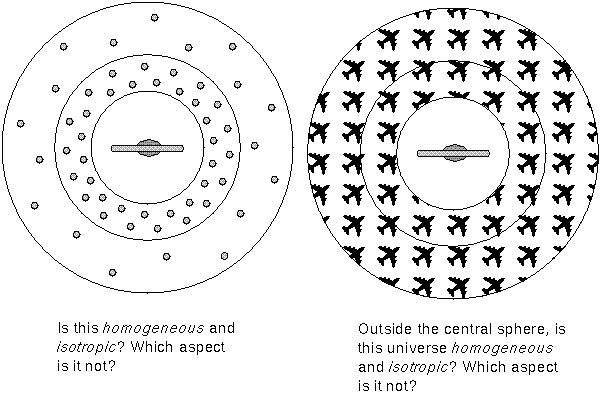
On size scales of billions of light years, the universe is assumed to be uniform. This makes the universe models simpler and ``more reasonable''---if we lived in an unusual part of the universe, then it would be almost impossible to understand the universe as a whole from observing our surroundings. The discovery of the long superclusters may seem to endanger this assumption. On large enough scales though, the universe has many superclusters in all directions. It is like a large bowl of tapioca pudding, one spoonful of pudding looks like any other spoonful, even though, there are the small tapioca pieces.
The idea of a uniform universe is called the cosmological principle. There are two aspects of the cosmological principle:

The cosmological principle is a Copernican idea. It means we are not in a special place. Every observer at a given cosmological time will see the same thing, such as the same Hubble-Lemaître law. ``Cosmological time'' in this context means the time measured from some common event like the creation of the universe. Everyone at the same cosmological time will measure the same age of the universe. The cosmological principle allows the universe to change, or evolve, throughout time.
An extension of the cosmological principle called the perfect cosmological principle says that the universe also does not change with time; there is no evolution. Therefore, in an expanding universe, new matter must be continually created. This violates a central rule of nature known as the law of the conservation of mass. This law says that the total amount of mass does not change---mass is not created from nothing or destroyed. However, the amount of new matter that would need to be created for the perfect cosmological principle to be true is quite small---only one hydrogen atom per cubic centimeter every 1015 years. This is approximately one hydrogen atom/Houston Astrodome every year---a very small amount! As described in the previous chapter, the increase in the number of quasars at large distances from us, is strong evidence of a universe that DOES change, or evolve. Other evidence for a changing universe is given later in this chapter.
To help you understand what curved spacetime means, let's use the analogy of a two-dimensional world curving into the third dimension. Pretend you are confined to the surface of a balloon and you only know about ``front'', ``back'', ``left'', and ``right'', but not ``up'' and ``down''. In your 2D universe you cannot see the third dimension. Your universe appears flat. Yet you know that your 2D universe must be curved because if you walk in a straight line, you eventually arrive back at where you started! The balloon universe has a finite size but no edge. You also know that the angles of large triangles add up to a number larger than 180°! For example, on the balloon the lines of longitude running north-south intercept the equator at a 90° angle and converge at the poles. So a triangle made of one point on the equator + the north pole + another point on the equator will have the angles add up to more than 180°. In a truly flat universe, the angles would add up to exactly 180°. You would be able to deduce that your universe is positively curved.
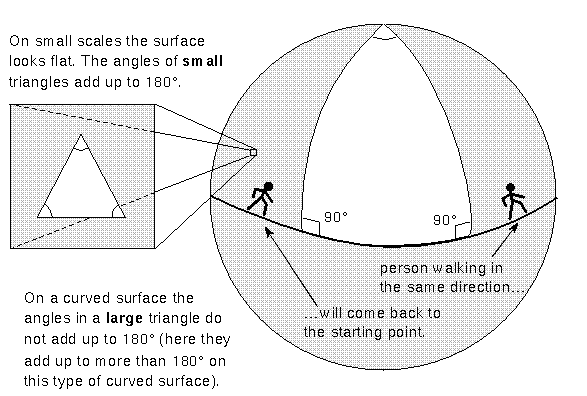
On sufficiently small scales the surface looks flat so the regular geometry rules apply. The angles in a small triangle add up to 180°. Here on the surface of the Earth, the Earth looks flat to us because the curvature of the Earth is so much larger than we are. The universe does not have to curve back on itself as shown in the illustrations above. This type of positively-curved universe is usually easier to picture, but the curvature could be the opposite. In a negatively-curved universe, the universe curves away from itself. A two-dimensional analogy would look like a saddle. The angles in large triangles would add up to less than 180°. Like the positively-curved universe, there would be no center on the surface and no edge.
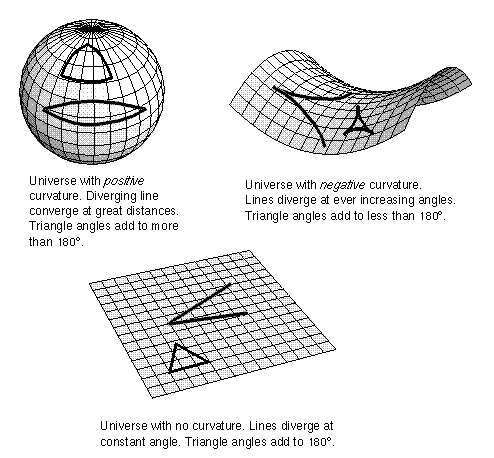
Rather than setting up BIG triangles in the universe, astronomers can use how the number of galaxies increases with increasing distance. If the universe has zero curvature and the galaxies are spread roughly uniformly in the universe, then the number of galaxies should increase linearly with ever greater volume. Lines defining an angle spread out in straight lines. If the universe has positive curvature, then the number of galaxies increases with greater volume then decreases with very large volumes. Lines defining an angle spread out at first and then converge at great distances. If the universe has negative curvature, then the number of galaxies increases more rapidly with ever greater volume than a flat universe. Lines defining an angle diverge at increasing angles as the lines curve away from each other. Simple in principle but in reality, it is hard to do.
Because the curvature is very small, we would need to look to very great distances to see a change from the flat universe case and distant objects are very faint and difficult to measure accurately. If we tried to look at how galaxy sizes changed with distance, we would face more than just measurement uncertainties. For example, in a positively-curved universe, very distant galaxies (ones with high redshift) would appear larger than in a flat universe but in our universe, there is no standard size for galaxies and we know that galaxies have changed over time through all sorts of interactions. Using how the apparent brightness of certain objects change with distance might work if you can find objects with a standardized luminosity (standard candles). In a positively-curved universe, the standard candles would appear brighter because the light rays would diverge more slowly than in a flat universe. Type Ia supernovae might work but the great distances needed for a universe with only very slight curvature, means even these supernovae are going to be very faint and difficult to measure accurately.
The idea of a curved surface also explains why astronomers in every galaxy will see the other galaxies moving away from it and, therefore, derive the same Hubble-Lemaître Law. Go back to the balloon analogy, imagine that there are flat houses on it. As the balloon expands, the elastic material moves the houses apart from each other. A person sitting on their front porch see everybody else moving away from her and she appears to be the center of the expansion.

Now add another dimension and you have our situation. Just like there is not new balloon material being created in the 2D analogy, new three-dimensional space is not being created in the expansion. Like any analogy, though, the balloon analogy has its limits. In the analogy, the balloon expands into the region around it---there is space beyond the balloon. However, with the expanding universe, space itself is expanding in three dimensions---the whole coordinate system is expanding. Our universe is NOT expanding ``into'' anything ``beyond''.
The expansion of space can have some surprising implications for astronomy professionals and students alike because our Newtonian view of a fixed coordinate grid in space is so much a part of our everyday experience on Earth. Charles Lineweaver and Tamara Davis wrote a nicely-illustrated article in the March 2005 issue of Scientific American on common misconceptions about the expansion of the universe such as: the galaxies are moving through space already present (they are not), galaxies cannot move away from us faster than light (they can), the size of the observable universe is the speed of light multiplied by the expansion time (the observable universe is much larger than that), and others. (Local PDF copy available here)
![]() Go back to previous section --
Go back to previous section --
![]() Go to next section
Go to next section
last updated: June 28, 2022